The MNIST dataset, comprising of handwritten digits from 0-9 is often used as an examplar for deep learning. This project will focus on the implementation and evaluation of the principles of deep learning, initially looking at perceptrons before introducing more complex networks and auto-encoders.

The Dataset

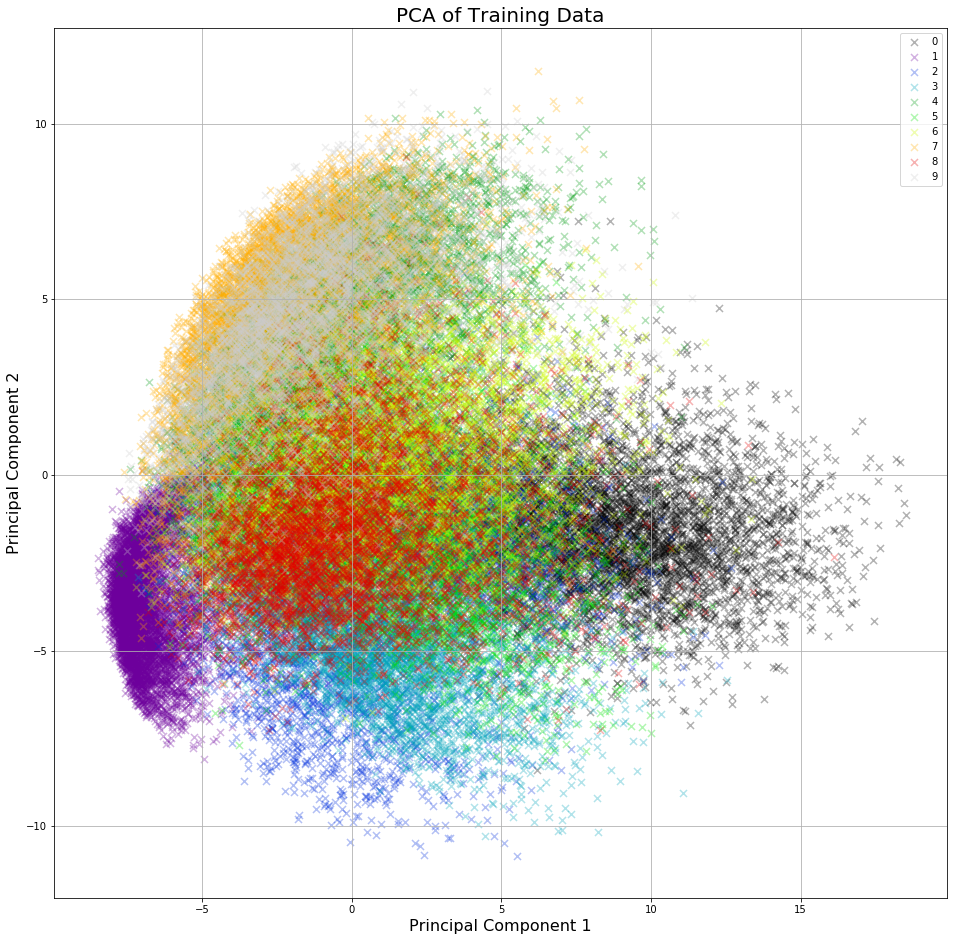
Before implementing anything it helps to look at the dataset. Since each pixel (of which there are 784) is a feature of the data this is not possible to visualise without first performing principal component analysis (PCA) - this can be seen below.

Perceptrons

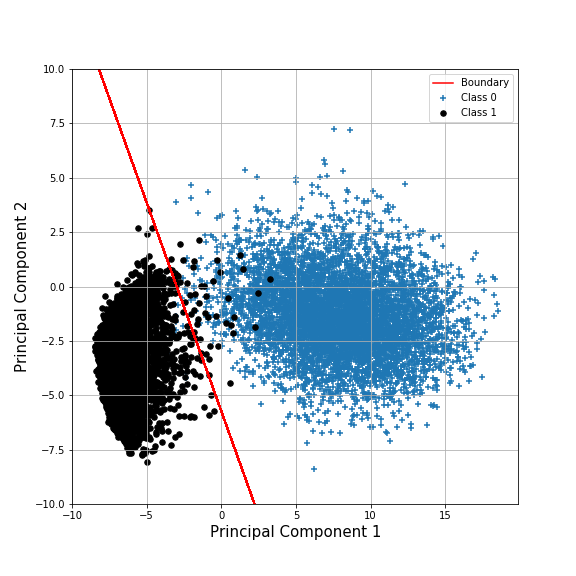
This visual helps to highlight the relative similarity between each class (digit) within the dataset. Understanding of a perceptron, a supervised binary classifier means we must focus on two classes from the dataset. The perceptron learns via a threshold function (defined below), optimising the predicitive weights by using the difference between predicted and absolute target values. The perceptron is capable of learning within a few iterations for classes 0 and 1.

$$ {\displaystyle f(\mathbf {x} )={\begin{cases} 1&{\text{if }}\ \mathbf {w} \cdot \mathbf {x} +b\geq0,\\-1&{\text{otherwise}}\end{cases}}} $$

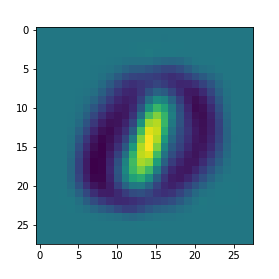
The figure below highlights that the weights havee learned to differentiate between two classes with the 'brighter' regions corresponding to a higher likelihood of belonging to class '1'. A better way to visualise it would be to formulate the decision boundary between the two classes in the same 2D PCA space as before (see graph below). This helps to highlight how a perceptron works for a binary classification problem, but what about more complex features reliant on an equally more complex approximating function? That is a job for multi-layer perceptrons.